4  Is Algorithm Selection Worth It? Comparing Selecting Single Algorithms and Parallel Execution

The material of this chapter is based on the following publication:

H. Kashgarani and L. Kotthoff, “Is algorithm selection worth it? comparing selecting single algorithms and parallel execution,” in AAAI Workshop on Meta-Learning and MetaDL Challenge, vol. 140 of Proceedings of Machine Learning Research, pp. 58–64, PMLR, 2021.

This chapter provides an empirical evaluation of SAT18-EXP solver performance (from the SAT Competition 2018) when running in parallel with other solvers at different levels of parallelism. Using the collected data, we trained two performance models based on the solver’s sequential performance data and instance features. We then performed algorithm selection using these selectors to choose the best-predicted solver for each instance, comparing these results to running multiple solvers in parallel. The findings showed that algorithm selection is superior when many solvers run in parallel. The results in this chapter offer preliminary insights for this dissertation, highlighting the importance of selecting an instance-based subportfolio of solvers since, with fewer solvers, the overhead is minimal. The instance based subportfolio approach will be further developed in Chapter 4 and explored with variations in Chapter 5 and 6.

4.1 Abstract

For many practical problems, there is more than one algorithm or approach to solve them. Such algorithms often have complementary performance – where one fails, another performs well, and vice versa. Per-instance algorithm selection leverages this by employing portfolios of complementary algorithms to solve sets of difficult problems, choosing the most appropriate algorithm for each problem instance. However, this requires complex models to effect this selection and introduces overhead to compute the data needed for those models. On the other hand, even basic hardware is more than capable of running several algorithms in parallel. We investigate the tradeoff between selecting a single algorithm and running multiple in parallel and incurring a slowdown because of contention for shared resources. Our results indicate that algorithm selection is worth it, especially for large portfolios.

4.2 Introduction

The performance of algorithms can vary significantly on different problem instances and there is no single algorithm that performs well in all cases. We can take advantage of such performance differences and create algorithm portfolios to combine the complementary strengths of different algorithms (C. Gomes and Selman 2001). From this portfolio, we can choose the algorithm with the best performance for each problem instance – this is known as the algorithm selection problem (Rice 1976). This is usually done by using machine learning methods and features extracted from the instances (Kotthoff 2014). Like all machine learning models, such approaches to algorithm selection make mistakes and in some cases choose an algorithm that does not have optimal performance. We can avoid this by exploiting modern multi-core architectures and simply running all algorithms in the portfolio in parallel, see e.g. (Amadini, Gabbrielli, and Mauro 2015a). While in theory optimal in terms of achieved performance, in practice contention for shared resources such as memory and caches reduces overall performance.

We present, to the best of our knowledge, the first investigation into the practical implications of running a large number of algorithms in parallel. We show the trade-off between algorithm selection that chooses a single algorithm and exploiting parallel resources and demonstrate that simply running all algorithms in a portfolio in parallel is not a panacea.

4.3 Background

Algorithm selection and other portfolio-based approaches have been applied in many areas of AI to improve performance. The first paper to introduce portfolios for solving hard AI problem considered a relatively simple parallel approach that executes all algorithms in the portfolio at the same time and stops them all as soon as the solution has been found by one (Huberman, Lukose, and Hogg 1997). (C. Gomes and Selman 2001; Hamadi, Jabbour, and Sais 2009) evaluate this strategy for stochastic algorithms and demonstrate that the variance of the time required to solve a problem decreases as the number of parallel runs increases.

This led to further approaches that take advantage of parallel processing by having several algorithms work independently or in cooperation on a given problem instance. (Yun and Epstein 2012) construct algorithm portfolios for constraint satisfaction problems that are executed in parallel and show performance improvements for up to 16 processors, and (Amadini, Gabbrielli, and Mauro 2015a) propose parallel portfolios with a dynamic schedule for up to 8 cores. Similarly, (Bordeaux, Hamadi, and Samulowitz 2009) show that by splitting the search space into sub-spaces, constraint solving portfolio approaches can take advantage of as many as 128 processors to achieve performance improvements.

For the Boolean satisfiability problem (SAT), simple static hand-crafted parallel portfolios have been studied by (Roussel 2012a) and (Wotzlaw et al. 2012) combined with a computed resource allocation for each solver. They employ a fixed selection of SAT solvers with good performance independently in parallel for a given number of cores. (Gagliolo and Schmidhuber 2006) introduce the dynamic algorithm portfolios that run a portfolio of algorithms with different shares of parallel processors along with an online time allocation learning approach. This includes a lifelong-learning approach in which the priority of algorithms is continually updated based on new runtime information. (Petrik and Zilberstein 2006) also propose a method for enhancing the performance of deterministic algorithms by running multiple algorithms in parallel for the same problem instance. (Kadioglu et al. 2011; Malitsky et al. 2012a) propose a more sophisticated approach. They select algorithms through an improved k-nearest-neighbor approach and use both dynamic and static scheduling for multiple algorithms from the portfolio to improve the chance that a particular problem instance will be solved within a time limit.

Similarly, (M. Lindauer, Hoos, and Hutter 2015) investigate parallel portfolio selection, and (H. H. Hoos et al. 2015) propose an approach to optimally schedule algorithms from a portfolio using answer set programming, while (Gonard, Schoenauer, and Sebag 2019) take the simpler approach of running a small portfolio of algorithms in parallel for a short amount of time and using algorithm selection to tackle any problem instances that remain unsolved after that. To the best of our knowledge, all previous research has only simulated parallel execution without measuring the actual performance. We investigate the practical ramifications of running more than one algorithm in parallel.

4.4 Experimental Setup

We run algorithms sequentially and with varying degrees of parallelism. We build and evaluate algorithm selection models for sequential execution to be able to compare selecting a single algorithm to run multiple in parallel. We measure performance in terms of penalized average runtime with factor 10 (PAR10) and misclassification penalty (MCP). The PAR10 score is the observed performance unless an algorithm timed out on a particular instance, when the timeout multiplied by the penalization factor is assumed as the runtime. The misclassification penalty is the difference between the performance of the algorithm that was run and the optimal algorithm on the same instance, i.e. it is always zero for the optimal algorithm.

We compare to the virtual best solver (VBS), which is the optimal algorithm from the portfolio for each problem instance to solve (cumulative misclassification penalty zero), and the single best solver (SBS), which is the algorithm from the portfolio with the best average performance across the entire set of problem instances to solve. The performance of the overhead-free parallel portfolio corresponds to the VBS.

We consider algorithms and problem instances from SAT, a popular application area for algorithm selection. We selected all 400 instances from the main track of the SAT Competition 2018 (Heule, Järvisalo, and Suda 2019) and computed their features using the SATzilla feature computation code (Xu et al. 2008). We exclude 19 instances for which we were unable to extract features within two hours of computational time, for a total of 381 problem instances.

Our solvers also come from the main track of the 2018 SAT competition; we consider all 39 submitted solvers for a total of 14,859 algorithm runs. We use the same time limit as in the SAT competition; 5000 CPU seconds for solving a single instance. However, we allowed 128 GB of RAM; more than five times what was allowed in the competition. During the parallel runs, the total amount of memory is shared among all running algorithms. We run the algorithms sequentially, 10 in parallel, 20 in parallel, 30 in parallel, and 32 in parallel to fully saturate a machine with 32 cores.

We leverage the algorithm selection benchmark library ASlib (Bischl, Kerschke, et al. 2016) and the LLAMA algorithm selection toolkit (Kotthoff 2013) for our algorithm selection experiments. We build regression models that predict the performance of each algorithm in the portfolio individually and select the algorithm with the best-predicted performance, and pairwise regression models that predict the performance difference for each pair of algorithms and select the algorithm with the aggregated best performance difference. We removed constant-valued (and therefore irrelevant) instance features and imputed missing feature values as the mean over all non-missing values of the feature.

For both regression and pairwise regression approaches, we use random forests as the base machine learning models. We tune their hyperparameters following (Bischl, Kerschke, et al. 2016); we consider values of 10 to 200 for the ntree hyperparameter and 1 to 30 for mtry. We optimize the hyperparameters using random search with 250 iterations and perform a nested cross-validation with 10 external and three internal folds to ensure unbiased performance measurements. All other hyperparameters were left at their default values.

# parallel runs	# timeouts	# out of memory errors
1	6982 (47%)	0 (0%)
10	10281 (69.19%)	6 (0.04%)
20	11853 (79.77%)	20 (0.13%)
30	12590 (84.73%)	27 (0.18%)
32	12715 (85.57%)	5 (0.03%)

4.5 Results

metric	# parallel runs	VBS	SBS	regression	pairwise regression
PAR10	1	9256.089	17585.66	13004.31	12588.44
	10	13062.16	27251.34	19888.25	20410.18
	20	17099.23	33630.54	25233.38	24970.07
	30	19970.29	36498.11	28628.15	27317.29
	32	21674.1	37285.5	29937.23	28888.24
MCP	1	0	1006.738	441.0526	379.5133
	10	0	1433.268	684.2932	733.7837
	20	0	1649.426	811.264	784.1721
	30	0	1645.936	862.5388	732.7824
	32	0	1556.284	822.1427	718.0386

Performance in terms of PAR10 score and misclassification penalty for different numbers of algorithms run in parallel. The VBS is the performance of the parallel portfolio; SBS is shown for comparison. The regression and pairwise regression bars show the performance of the respective algorithm selection models. We omit the plot for VBS performance in terms of MCP score as it is always zero by definition.

We first evaluate the effect the number of parallel runs has on what fraction of all algorithm runs is successful. Table [tab:errors] shows the number and percentage of unsuccessful runs at each level of parallelism. With only one algorithm running at a time, 47% of runs fail with a timeout. This increases as more and more algorithms are run in parallel. Similarly, the number of runs that fail because they run out of memory increases, as more and more runs share the same amount of physical memory. This does not significantly affect the results though, as even in the worst-case much less than 1% of the total number of runs is affected. Parallel runs have a much more significant effect on the number of timeouts though – from 47% runs that exceeded the available time when only a single algorithm is running at a time, we see an increase to 85.57% of total runs when 32 algorithms are run in parallel. Altogether, 85.6% of runs either time out or run out of memory when 32 algorithms are running in parallel; a significant increase over running only a single algorithm.

Table [tab:values] and Figure 1.1 show the performance we observed for all parallelism levels and approaches we consider. The PAR10 score for the VBS increases significantly as we increase the number of algorithms run in parallel; \(\approx\)41% from one to 10 parallel runs. Similarly, the score for the single best solver increases by \(\approx\)55% for the same interval. The PAR10 score is more than twice as high for 32 parallel runs compared to a single run for both VBS and SBS – contention for shared resources has a significant impact on the time it takes to solve a set of instances. A large contributor to the increase in PAR10 score is the increased number of unsuccessful runs because of timeouts or memory outs.

We observe a similar decrease in performance as for the VBS and SBS for the algorithm selection approaches as the level of parallelism increases – in fact, we observe even steeper performance losses in the beginning, with \(\approx\)53% performance decrease from one algorithm to 10 for regression models and \(\approx\)62% for pairwise regression models in terms of PAR10. However, we observe a performance increase for both approaches (lower MCP scores) when going from 30 algorithms run in parallel to 32, and a performance increase for pairwise regression model when going from 20 algorithms run in parallel to 30. It is unclear what exactly causes this performance increase; it is likely that the machine learning task that underlies the selection process becomes easier as more algorithms lose competitiveness because of timeouts and memory limits.

Percentage increase in terms of PAR10 score for running different numbers of algorithms in parallel compared to algorithm selector performance for choosing a single algorithm. For example, an increase of 100% means that running the algorithms in parallel doubles the PAR10 score over selecting a single algorithm.

Our results show that algorithm selection for choosing a single algorithm to run can beat parallel execution in practice for a large number of solvers. Figure 1.2 shows that the performance of both the regression and pairwise regression algorithm selection approaches are better than the VBS for any level of parallelism beyond running a single algorithm. Both in terms of PAR10 and MCP, algorithm selection is always better than the single best solver. When using all 32 cores we have available, the VBS becomes more than 66% worse than the regression algorithm selection approach and more than 72% worse than the pairwise regression algorithm selection approach. Even when running only 10 algorithms at the same time (and assuming that we know which 10 of the 39 total algorithms to run to maximize performance), the VBS is more than 0.4% and 3% worse than regression and pairwise regression approaches, respectively.

While the overhead-free parallel portfolio promises optimal performance, in theory, we clearly see that in practice this is not the case – contention for shared resources and physical limits of the machine that is used to run the algorithms has a significant detrimental effect on performance. Even though algorithm selection models are not perfect, they outperform actual parallel portfolios in terms of observed performance even for a relatively small number of algorithms run in parallel.

4.6 Conclusions and Future Work

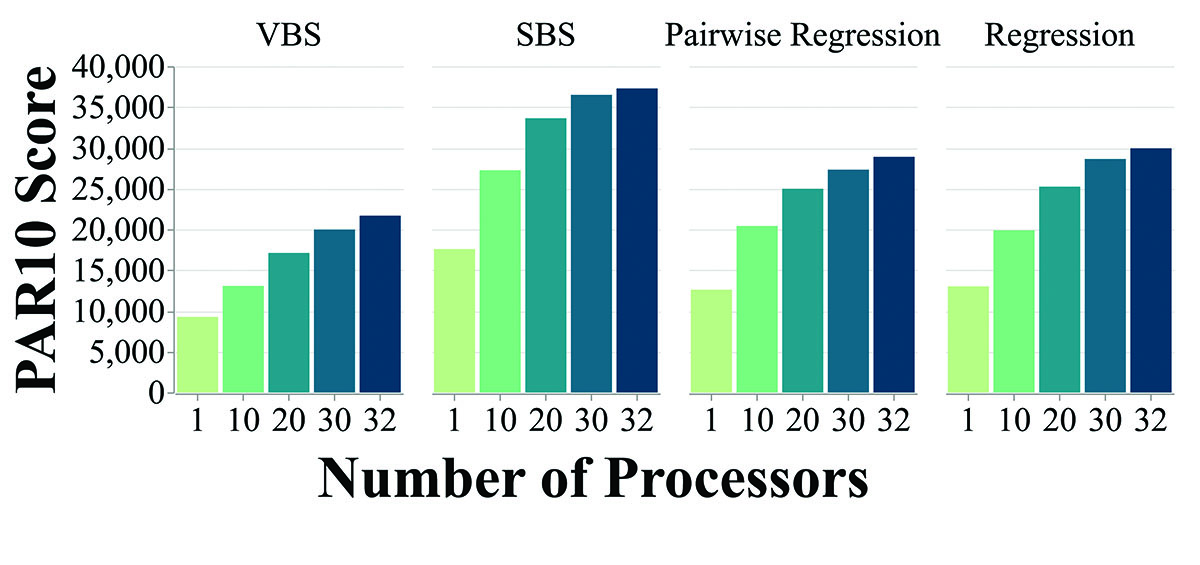
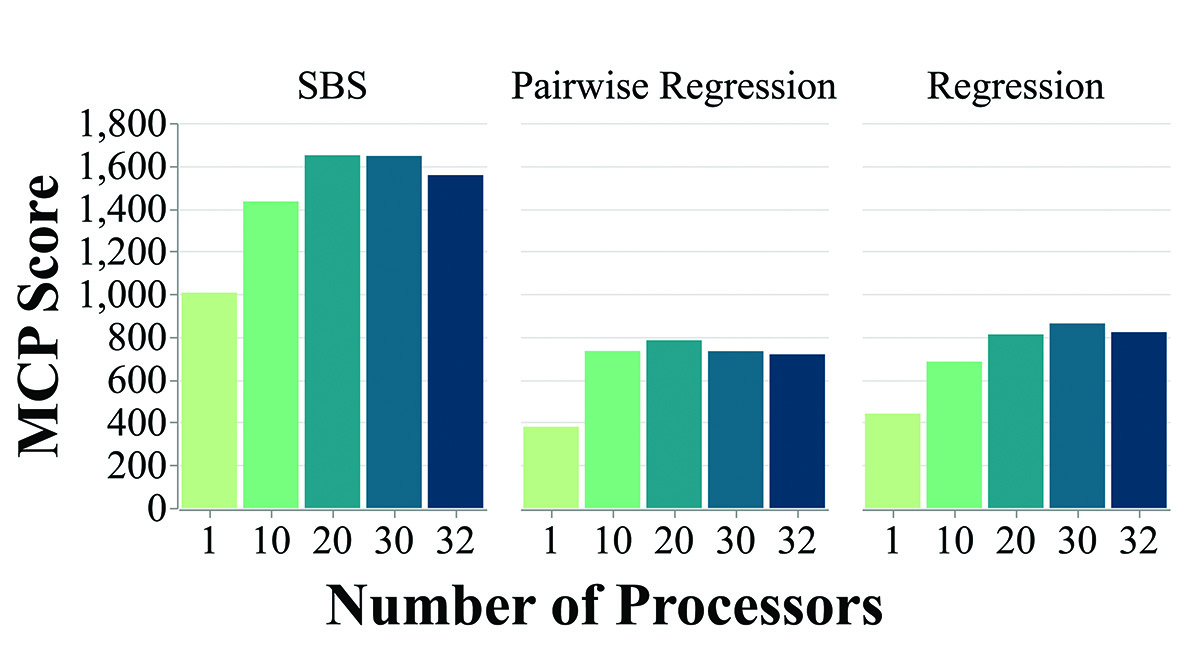
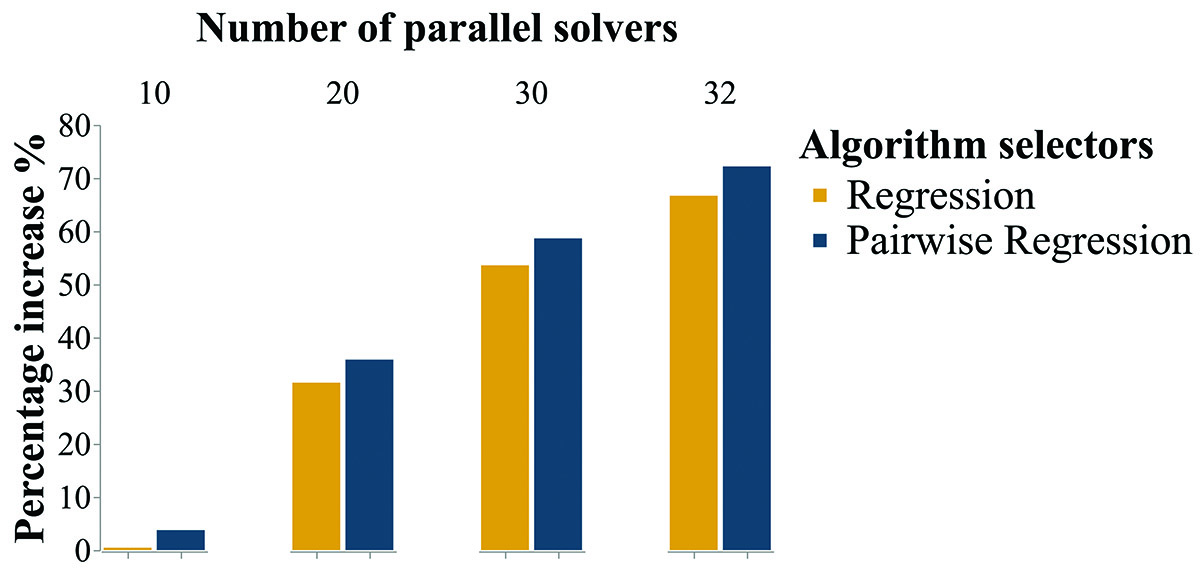
We investigated the actual observed performance of parallel portfolios, in contrast to their theoretical performance that is usually used in the literature. We found that running even a relatively small number of algorithms in parallel on the same machine can have a significant negative impact on overall performance. Algorithm selection on the other hand chooses only a single algorithm and is able to achieve better overall performance, even though its predictions are not perfect and it does not always choose the algorithm with the best performance for solving a given problem instance.

An obvious avenue for future work is a hybrid approach to what we present here, where instead of a single algorithm several are chosen to run in parallel. Existing literature proposes a multitude of methods for doing so; however, none of these approaches have been evaluated as in the investigation we present here – by actually running more than one algorithm in parallel and observing the performance rather than simulating this based on the performance observed when only a single algorithm is run at a time. In addition, there is scope for developing new approaches for dynamic resource allocation for algorithm selection.

Aigner, Martin, Armin Biere, Christoph M. Kirsch, Aina Niemetz, and Mathias Preiner. 2013a. “Analysis of Portfolio-Style Parallel SAT Solving on Current Multi-Core Architectures.” In POS-13. Fourth Pragmatics of SAT Workshop, a Workshop of the SAT 2013 Conference, July 7, 2013, Helsinki, Finland, edited by Daniel Le Berre, 29:28–40. EPiC Series in Computing. EasyChair. https://doi.org/10.29007/73N4.

Aigner, Martin, Armin Biere, Christoph M Kirsch, Aina Niemetz, and Mathias Preiner. 2013b. “Analysis of Portfolio-Style Parallel SAT Solving on Current Multi-Core Architectures.” POS@ SAT 29: 28–40.

Ali, Shawkat, and Kate A Smith. 2006. “On Learning Algorithm Selection for Classification.” Applied Soft Computing 6 (2): 119–38.

Amadini, Roberto, Maurizio Gabbrielli, and Jacopo Mauro. 2014. “SUNNY: A Lazy Portfolio Approach for Constraint Solving.” Theory Pract. Log. Program. 14 (4-5): 509–24. https://doi.org/10.1017/S1471068414000179.

———. 2015a. “A Multicore Tool for Constraint Solving.” In Proceedings of the 24th International Conference on Artificial Intelligence, 232–38.

———. 2015b. “Why CP Portfolio Solvers Are (under)Utilized? Issues and Challenges.” In Logic-Based Program Synthesis and Transformation, edited by Moreno Falaschi, 349–64. Cham: Springer International Publishing.

———. 2018. “SUNNY-CP and the MiniZinc Challenge.” Theory and Practice of Logic Programming 18 (1): 81–96. https://doi.org/10.1017/S1471068417000205.

Arbelaez, Alejandro, Youssef Hamadi, and Michele Sebag. 2009. “Online heuristic selection in constraint programming.”

Bacchus, Fahiem, Matti Jarvisalo, and Ruben Martins. 2019. MaxSAT Evaluation 2019.

Balyo, Tomas, Nils Froleyks, Marijn Heule, Markus Iser, Matti Järvisalo, and Martin Suda, eds. 2021. Proceedings of SAT Competition 2021: Solver and Benchmark Descriptions. Anthology or special issue. Department of Computer Science Report Series b. Department of Computer Science Report Series B. http://hdl.handle.net/10138/333647.

Balyo, Tomas, Marijn Heule, Markus Iser, Matti Järvisalo, and Martin Suda, eds. 2023. Proceedings of SAT Competition 2023: Solver, Benchmark and Proof Checker Descriptions. Anthology or special issue. Department of Computer Science, Helsinki Institute for Information Technology, Constraint Reasoning; Optimization research group / Matti Järvisalo.

Balyo, Tomáš, Marijn J H Heule, and Matti Järvisalo. 2017. “SAT Competition 2017 Solver and Benchmark Descriptions.” Proceedings of SAT COMPETITION 2017, 14–15.

Batista dos Santos, Vânia, and Luiz Henrique de Campos Merschmann. 2020. “Metalearning Applied to Multi-Label Text Classification.” In Proceedings of the XVI Brazilian Symposium on Information Systems. SBSI ’20. New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/3411564.3411646.

Biere, Armin. 2012. “Lingeling and friends entering the SAT challenge 2012.” Department of Computer Science Series of Publications B, January, 33–34.

———. 2013. “Lingeling, Plingeling and Treengeling Entering the SAT Competition 2013.” In. https://api.semanticscholar.org/CorpusID:972178.

Biere, Armin, Marijn Heule, Hans van Maaren, and Toby Walsh. 2009. “Conflict-Driven Clause Learning Sat Solvers.” Handbook of Satisfiability, Frontiers in Artificial Intelligence and Applications, 131–53.

———, eds. 2021. Handbook of Satisfiability - Second Edition. Vol. 336. Frontiers in Artificial Intelligence and Applications. IOS Press. https://doi.org/10.3233/FAIA336.

Bischl, Bernd, Pascal Kerschke, Lars Kotthoff, Marius Lindauer, Yuri Malitsky, Alexandre Fréchette, Holger Hoos, et al. 2016. “ASlib: A Benchmark Library for Algorithm Selection.” Artificial Intelligence 237: 41–58.

Bischl, Bernd, Michel Lang, Lars Kotthoff, Julia Schiffner, Jakob Richter, Erich Studerus, Giuseppe Casalicchio, and Zachary M. Jones. 2016. “mlr: Machine Learning in R.” Journal of Machine Learning Research 17 (170): 1–5. https://jmlr.org/papers/v17/15-066.html.

Bischl, Bernd, Raphael Sonabend, Lars Kotthoff, and Michel Lang, eds. 2024. Applied Machine Learning Using mlr3 in R. CRC Press. https://mlr3book.mlr-org.com.

Bishop, Christopher M, and Nasser M Nasrabadi. 2006. Pattern Recognition and Machine Learning. Vol. 4. 4. Springer.

Bordeaux, Lucas, Youssef Hamadi, and Horst Samulowitz. 2009. “Experiments with Massively Parallel Constraint Solving.” In Proceedings of the 21st International Jont Conference on Artifical Intelligence, 443–48. IJCAI’09. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.

Brazdil, P., J. N. van Rijn, C. Soares, and J. Vanschoren. 2022. Metalearning: Applications to Automated Machine Learning and Data Mining. Cognitive Technologies. Springer International Publishing. https://books.google.com/books?id=zDcOzgEACAAJ.

Breiman, Leo. 2001. “Random Forests.” Machine Learning 45: 5–32.

Brighton, Henry, and Chris Mellish. 2002. “Advances in Instance Selection for Instance-Based Learning Algorithms.” Data Mining and Knowledge Discovery 6: 153–72.

Carchrae, Tom, and J. Christopher Beck. 2005. “Applying Machine Learning to Low-Knowledge Control of Optimization Algorithms.” Computational Intelligence 21. https://api.semanticscholar.org/CorpusID:7953876.

Cárdenas-Montes, Miguel. 2016. “Evaluating the Difficulty of Instances of the Travelling Salesman Problem in the Nearby of the Optimal Solution Based on Random Walk Exploration.” In Hybrid Artificial Intelligent Systems, edited by Francisco Martínez-Álvarez, Alicia Troncoso, Héctor Quintián, and Emilio Corchado, 299–310. Cham: Springer International Publishing.

Cenamor, Isabel, Tomás De La Rosa, and Fernando Fernández. 2013. “Learning Predictive Models to Configure Planning Portfolios.” In Proceedings of the 4th Workshop on Planning and Learning (ICAPS-PAL 2013), 14–22. Citeseer.

———. 2016. “The IBaCoP planning system: instance-based configured portfolios.” J. Artif. Int. Res. 56 (1): 657–91.

Cenamor, Isabel, Tomás de la Rosa, Fernando Fernández, et al. 2014. “IBACOP and IBACOP2 planner.” IPC 2014 Planner Abstracts, 35–38.

Ciorba, Florina M., Ali Mohammed, Jonas H. Müller Korndörfer, and Ahmed Eleliemy. 2023. “Automated Scheduling Algorithm Selection in OpenMP.” In 2023 22nd International Symposium on Parallel and Distributed Computing (ISPDC), 106–9. https://doi.org/10.1109/ISPDC59212.2023.00025.

Collautti, Marco, Yuri Malitsky, Deepak Mehta, and Barry O’Sullivan. 2013. “SNNAP: Solver-based nearest neighbor for algorithm portfolios.” In Machine Learning and Knowledge Discovery in Databases: European Conference, ECML PKDD 2013, Prague, Czech Republic, September 23-27, 2013, Proceedings, Part III 13, 435–50. Springer.

Collevati, M., Agostino Dovier, and A. Formisano. 2022. “GPU Parallelism for SAT Solving Heuristics.” CEUR-WS.

Davis, John D., Zhangxi Tan, Fang Yu, and Lintao Zhang. 2008. “A Practical Reconfigurable Hardware Accelerator for Boolean Satisfiability Solvers.” In 2008 45th ACM/IEEE Design Automation Conference, 780–85. https://doi.org/10.1145/1391469.1391669.

Davis, Martin, George Logemann, and Donald Loveland. 1962. “A Machine Program for Theorem-Proving.” Commun. ACM 5 (7): 394–97. https://doi.org/10.1145/368273.368557.

Ewald, Roland, Adelinde M. Uhrmacher, and Kaustav Saha. 2010. “Data Mining for Simulation Algorithm Selection.” In. ICST. https://doi.org/10.4108/ICST.SIMUTOOLS2009.5659.

Fawcett, Chris, Mauro Vallati, Frank Hutter, Jörg Hoffmann, Holger Hoos, and Kevin Leyton-Brown. 2014. “Improved Features for Runtime Prediction of Domain-Independent Planners.” Proceedings of the International Conference on Automated Planning and Scheduling 24 (1): 355–59. https://doi.org/10.1609/icaps.v24i1.13680.

Froleyks, Nils, Marijn Heule, Markus Iser, Matti Järvisalo, and Martin Suda. 2021. “SAT Competition 2020.” Artificial Intelligence 301: 103572. https://doi.org/https://doi.org/10.1016/j.artint.2021.103572.

Gagliolo, Matteo, and Jürgen Schmidhuber. 2006. “Dynamic algorithm portfolios.” Annals of Mathematics and Artificial Intelligence 47: 3–4.

Gebser, Martin, Roland Kaminski, Benjamin Kaufmann, Torsten Schaub, Marius Thomas Schneider, and Stefan Ziller. 2011. “A Portfolio Solver for Answer Set Programming: Preliminary Report.” In Logic Programming and Nonmonotonic Reasoning, edited by James P. Delgrande and Wolfgang Faber, 352–57. Berlin, Heidelberg: Springer Berlin Heidelberg.

GEBSER, MARTIN, MARCO MARATEA, and FRANCESCO RICCA. 2019. “The Seventh Answer Set Programming Competition: Design and Results.” Theory and Practice of Logic Programming 20 (2): 176–204. https://doi.org/10.1017/s1471068419000061.

Gerevini, Alfonso, and Derek Long. 2005. “Plan constraints and preferences in PDDL3.” Technical Report 2005-08-07, Department of Electronics for Automation ….

Gil, Luı́s, Paulo F. Flores, and Luı́s Miguel Silveira. 2009. “PMSat: a parallel version of MiniSAT.” J. Satisf. Boolean Model. Comput. 6 (1-3): 71–98. https://doi.org/10.3233/SAT190063.

Gomes, Carla Pedro, and Bart Selman. 1997. “Algorithm Portfolio Design: Theory Vs. Practice.” ArXiv abs/1302.1541. https://api.semanticscholar.org/CorpusID:8512615.

Gomes, Carla, and Bart Selman. 2001. “Algorithm Portfolios.” Artificial Intelligence 126: 43–62.

Gonard, François, Marc Schoenauer, and Michèle Sebag. 2019. “Algorithm Selector and Prescheduler in the ICON Challenge.” In Bioinspired Heuristics for Optimization, 203–19. Springer International Publishing.

Gulati, Kanupriya, Suganth Paul, Sunil P. Khatri, Srinivas Patil, and Abhijit Jas. 2009. “FPGA-based hardware acceleration for Boolean satisfiability.” ACM Trans. Des. Autom. Electron. Syst. 14 (2). https://doi.org/10.1145/1497561.1497576.

Guo, Haipeng, and William H. Hsu. 2003. “Algorithm Selection for Sorting and Probabilistic Inference: A Machine Learning-Based Approach.” PhD thesis, USA: Kansas State University.

———. 2005. “A Learning-Based Algorithm Selection Meta-Reasoner for the Real-Time MPE Problem.” In AI 2004: Advances in Artificial Intelligence, edited by Geoffrey I. Webb and Xinghuo Yu, 307–18. Berlin, Heidelberg: Springer. https://doi.org/10.1007/978-3-540-30549-1_28.

Hamadi, Youssef, Said Jabbour, and Lakhdar Sais. 2009. “ManySAT: a Parallel SAT Solver.” Journal on Satisfiability, Boolean Modeling and Computation. https://doi.org/10.3233/sat190070.

Heule, Marijn J. H., Matti Järvisalo, and Martin Suda. 2019. “SAT Competition 2018.” Journal on Satisfiability, Boolean Modeling and Computation. https://doi.org/10.3233/sat190120.

Hölldobler, Steffen, Norbert Manthey, and Ari Saptawijaya. 2010. “Improving Resource-Unaware SAT Solvers.” In Logic for Programming, Artificial Intelligence, and Reasoning, edited by Christian G. Fermüller and Andrei Voronkov, 519–34. Berlin, Heidelberg: Springer Berlin Heidelberg.

Hölldobler, Steffen, Norbert Manthey, Van Hau Nguyen, Julian Stecklina, and Peter Steinke. 2011. “A short overview on modern parallel SAT-solvers.” ICACSIS 2011 - 2011 International Conference on Advanced Computer Science and Information Systems, Proceedings, no. January: 201–6.

Hoos, Holger H., Roland Kaminski, Marius Thomas Lindauer, and Torsten Schaub. 2015. “aspeed: Solver scheduling via answer set programming.” TPLP 15 (1): 117–42.

Hoos, Holger H., and Thomas Stützle. 2005. “Propositional Satisfiability and Constraint Satisfaction.” In Stochastic Local Search, 257–312. The Morgan Kaufmann Series in Artificial Intelligence. San Francisco: Morgan Kaufmann. https://doi.org/https://doi.org/10.1016/B978-155860872-6/50023-8.

Hoos, Holger, Marius Lindauer, and Torsten Schaub. 2014. “Claspfolio 2: Advances in Algorithm Selection for Answer Set Programming.” https://arxiv.org/abs/1405.1520.

Howe, Adele E, Eric Dahlman, Christopher Hansen, Michael Scheetz, and Anneliese Von Mayrhauser. 2000. “Exploiting Competitive Planner Performance.” In Recent Advances in AI Planning: 5th European Conference on Planning, ECP’99, Durham, UK, September 8-10, 1999. Proceedings 5, 62–72. Springer.

Hu, Mengqi, Teresa Wu, and Jeffery D. Weir. 2012. “An Intelligent Augmentation of Particle Swarm Optimization with Multiple Adaptive Methods.” Information Sciences 213: 68–83. https://doi.org/https://doi.org/10.1016/j.ins.2012.05.020.

Huberman, Bernardo A., Rajan M. Lukose, and Tad Hogg. 1997. “An economics approach to hard computational problems.” Science 275 (5296): 51–54. https://doi.org/10.1126/science.275.5296.51.

Hutter, Frank, Lars Kotthoff, and Joaquin Vanschoren, eds. 2019. Automated Machine Learning - Methods, Systems, Challenges. Springer.

Hutter, Frank, Manuel López-Ibáñez, Chris Fawcett, Marius Lindauer, Holger H. Hoos, Kevin Leyton-Brown, and Thomas Stützle. 2014. “AClib: A Benchmark Library for Algorithm Configuration.” In Learning and Intelligent Optimization, edited by Panos M. Pardalos, Mauricio G. C. Resende, Chrysafis Vogiatzis, and Jose L. Walteros, 36–40. Cham: Springer International Publishing.

Hutter, Frank, Lin Xu, Holger H. Hoos, and Kevin Leyton-Brown. 2014. “Algorithm Runtime Prediction: Methods & Evaluation.” Artificial Intelligence 206: 79–111. https://doi.org/https://doi.org/10.1016/j.artint.2013.10.003.

Hyvarinen, Antti E. J., and Christoph M. Wintersteiger. 2012. “Approaches for Multi-Core Propagation in Clause Learning Satisfiability Solvers.” MSR-TR-2012-47. https://www.microsoft.com/en-us/research/publication/approaches-for-multi-core-propagation-in-clause-learning-satisfiability-solvers/.

Hyvärinen, Antti E. J., Tommi Junttila, and Ilkka Niemelä. 2008. “Strategies for Solving SAT in Grids by Randomized Search.” In Intelligent Computer Mathematics, edited by Serge Autexier, John Campbell, Julio Rubio, Volker Sorge, Masakazu Suzuki, and Freek Wiedijk, 125–40. Berlin, Heidelberg: Springer Berlin Heidelberg.

———. 2010. “Partitioning SAT Instances for Distributed Solving.” In Logic for Programming, Artificial Intelligence, and Reasoning, edited by Christian G. Fermüller and Andrei Voronkov, 372–86. Berlin, Heidelberg: Springer Berlin Heidelberg.

Hyvärinen, Antti E. J., and Norbert Manthey. 2012. “Designing Scalable Parallel SAT Solvers.” In Theory and Applications of Satisfiability Testing – SAT 2012, edited by Alessandro Cimatti and Roberto Sebastiani, 214–27. Berlin, Heidelberg: Springer Berlin Heidelberg.

Kadioglu, Serdar, Yuri Malitsky, Ashish Sabharwal, Horst Samulowitz, and Meinolf Sellmann. 2011. “Algorithm selection and scheduling.” Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 6876 LNCS: 454–69. https://doi.org/10.1007/978-3-642-23786-7_35.

Kadioglu, Serdar, Yuri Malitsky, Meinolf Sellmann, and Kevin Tierney. 2010. “ISAC–Instance-Specific Algorithm Configuration.” In ECAI 2010, 751–56. IOS Press.

Kadıoglu, Serdar, Yuri Malitsky, and Meinolf Sellmann. n.d. “How to Win Gold at a SAT Competition Without Writing a SAT Solver.”

Karp, Richard M. 1972. “Reducibility Among Combinatorial Problems.” In Complexity of Computer Computations: Proceedings of a Symposium on the Complexity of Computer Computations, Held March 20–22, 1972, at the IBM Thomas j. Watson Research Center, Yorktown Heights, New York, and Sponsored by the Office of Naval Research, Mathematics Program, IBM World Trade Corporation, and the IBM Research Mathematical Sciences Department, edited by Raymond E. Miller, James W. Thatcher, and Jean D. Bohlinger, 85–103. Boston, MA: Springer US. https://doi.org/10.1007/978-1-4684-2001-2_9.

Kashgarani, Haniye, and Lars Kotthoff. 2021. “Is Algorithm Selection Worth It? Comparing Selecting Single Algorithms and Parallel Execution.” In AAAI Workshop on Meta-Learning and MetaDL Challenge, 140:58–64. Proceedings of Machine Learning Research. PMLR. https://proceedings.mlr.press/v140/kashgarani21a.html.

———. 2023. “Automatic Parallel Portfolio Selection.” In ECAI 2023, 1215–22. IOS Press.

Kerschke, Pascal, Holger H. Hoos, Frank Neumann, and Heike Trautmann. 2019. “Automated Algorithm Selection: Survey and Perspectives.” Evolutionary Computation 27 (1): 3–45. https://doi.org/10.1162/evco_a_00242.

Kerschke, Pascal, Lars Kotthoff, Jakob Bossek, Holger H. Hoos, and Heike Trautmann. 2018. “Leveraging TSP Solver Complementarity through Machine Learning.” Evolutionary Computation 26 (4): 597–620. https://doi.org/10.1162/evco_a_00215.

Kocamaz, Uğur Erkin. 2013. “Increasing the Efficiency of Quicksort Using a Neural Network Based Algorithm Selection Model.” Information Sciences 229: 94–105. https://doi.org/https://doi.org/10.1016/j.ins.2012.11.014.

Kotthoff, Lars. 2013. “LLAMA: Leveraging Learning to Automatically Manage Algorithms.” CoRR abs/1306.1031. http://arxiv.org/abs/1306.1031.

———. 2014. “Algorithm selection for combinatorial search problems: A survey.” AI Magazine 35 (3): 48–69.

Kullback, S., and R. A. Leibler. 1951. “On Information and Sufficiency.” The Annals of Mathematical Statistics 22 (1): 79–86. http://www.jstor.org/stable/2236703.

Kuş, Erdem, Özgür Akgün, Nguyen Dang, and Ian Miguel. 2024. “Frugal Algorithm Selection.” Cornell University. https://doi.org/ 10.48550/arxiv.2405.11059 .

Le Frioux, Ludovic. 2019. “Towards more efficient parallel SAT solving.” Theses, Sorbonne Université. https://theses.hal.science/tel-03030122.

Leeson, Will, and Matthew B. Dwyer. 2024. “Algorithm Selection for Software Verification Using Graph Neural Networks.” ACM Trans. Softw. Eng. Methodol. 33 (3). https://doi.org/10.1145/3637225.

Leyton-Brown, Kevin, Eugene Nudelman, Galen Andrew, Jim McFadden, and Yoav Shoham. 2003. “A portfolio approach to algorithm selection.” In Proceedings of the 18th International Joint Conference on Artificial Intelligence, 1542–43. IJCAI’03. San Francisco, CA, USA: Morgan Kaufmann Publishers Inc.

Leyton-Brown, Kevin, Eugene Nudelman, and Yoav Shoham. 2002. “Learning the Empirical Hardness of Optimization Problems: The Case of Combinatorial Auctions.” In Principles and Practice of Constraint Programming - CP 2002, edited by Pascal Van Hentenryck, 556–72. Berlin, Heidelberg: Springer Berlin Heidelberg.

Lieder, Falk, Dillon Plunkett, Jessica B Hamrick, Stuart J Russell, Nicholas Hay, and Tom Griffiths. 2014. “Algorithm Selection by Rational Metareasoning as a Model of Human Strategy Selection.” In Advances in Neural Information Processing Systems, edited by Z. Ghahramani, M. Welling, C. Cortes, N. Lawrence, and K. Q. Weinberger. Vol. 27. Curran Associates, Inc. https://proceedings.neurips.cc/paper_files/paper/2014/file/7fb8ceb3bd59c7956b1df66729296a4c-Paper.pdf.

Lindauer, Marius, Rolf-David Bergdoll, and Frank Hutter. 2016. “An Empirical Study of Per-Instance Algorithm Scheduling.” In Proceedings of the Tenth International Conference on Learning and Intelligent Optimization, LION’16, in: Lecture Notes in Computer Science, 253–59. Springer; Springer.

Lindauer, Marius, Holger H Hoos, Frank Hutter, and Torsten Schaub. 2015. “Autofolio: An Automatically Configured Algorithm Selector.” Journal of Artificial Intelligence Research 53: 745–78.

Lindauer, Marius, Holger Hoos, and Frank Hutter. 2015. “From sequential algorithm selection to parallel portfolio selection.” In International Conference on Learning and Intelligent Optimization, 1–16. Springer.

Lindauer, Marius, Holger Hoos, Kevin Leyton-Brown, and Torsten Schaub. 2017. “Automatic Construction of Parallel Portfolios via Algorithm Configuration.” Artificial Intelligence 244: 272–90. https://doi.org/https://doi.org/10.1016/j.artint.2016.05.004.

Lindauer, Marius, Jan N. van Rijn, and Lars Kotthoff. 2017. “Open Algorithm Selection Challenge 2017: Setup and Scenarios.” In Proceedings of the Open Algorithm Selection Challenge, 79:1–7. PMLR. https://proceedings.mlr.press/v79/lindauer17a.html.

Lindauer, Marius, Jan N. van Rijn, and Lars Kotthoff. 2019. “The algorithm selection competitions 2015 and 2017.” Artificial Intelligence 272: 86–100. https://doi.org/https://doi.org/10.1016/j.artint.2018.10.004.

Lindauer, T Marius. 2014. “Algorithm selection, scheduling and configuration of Boolean constraint solvers.” PhD thesis, Universität Potsdam.

Lissovoi, Andrei, Pietro S. Oliveto, and John Alasdair Warwicker. 2019. “On the Time Complexity of Algorithm Selection Hyper-Heuristics for Multimodal Optimisation.” Proceedings of the AAAI Conference on Artificial Intelligence 33 (01): 2322–29. https://doi.org/10.1609/aaai.v33i01.33012322.

Liu, Wenwen, Shiu Yin Yuen, and Chi Sung. 2022. “A Generic Method to Compose an Algorithm Portfolio with a Problem Set of Unknown Distribution.” Memetic Computing 14 (September): 1–18. https://doi.org/10.1007/s12293-022-00367-8.

Lukac, Martin, and Michitaka Kameyama. 2023. “Verification Based Algorithm Selection.” In 2023 International Conference on Information and Digital Technologies (IDT), 25–30. https://doi.org/10.1109/IDT59031.2023.10194439.

Malitsky, Yuri, Barry O’Sullivan, Alessandro Previti, and Joao Marques-Silva. 2014. “A Portfolio Approach to Enumerating Minimal Correction Subsets for Satisfiability Problems.” In, 368–76. Springer, Cham. https://doi.org/ 10.1007/978-3-319-07046-9_26 .

Malitsky, Yuri, Ashish Sabharwal, Horst Samulowitz, and Meinolf Sellmann. 2012b. “Parallel SAT Solver Selection and Scheduling.” In Proceedings of the 18th International Conference on Principles and Practice of Constraint Programming - Volume 7514, 512–26. Springer-Verlag.

———. 2012a. “Parallel SAT solver selection and scheduling.” Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics) 7514 LNCS: 512–26. https://doi.org/10.1007/978-3-642-33558-7_38.

———. 2013. “Algorithm portfolios based on cost-sensitive hierarchical clustering.” In Proceedings of the Twenty-Third International Joint Conference on Artificial Intelligence, 608–14. IJCAI ’13. Beijing, China: AAAI Press.

Manthey, Norbert. 2011. “Parallel SAT solving-using more cores.” Pragmatics of SAT (POS’11).

Maratea, Marco, Luca Pulina, and Francesco Ricca. 2014. “A Multi-Engine Approach to Answer-Set Programming.” Theory and Practice of Logic Programming 14 (6): 841–68.

Martins, Ruben, Matti Jarvisalo, and Fahiem Bacchus. 2016. Proceedings of SAT Competition 2016 : Solver and Benchmark Descriptions. University of Helsinki.

Maturana, Jorge, Álvaro Fialho, Frédéric Saubion, Marc Schoenauer, Frédéric Lardeux, and Michèle Sebag. 2012. “Adaptive Operator Selection and Management in Evolutionary Algorithms.” In Autonomous Search, 161–89. Springer. https://doi.org/10.1007/978-3-642-21434-9_7.

Meyer, Quirin, Fabian Schönfeld, Marc Stamminger, and Rolf Wanka. 2010. “3-SAT on CUDA: Towards a massively parallel SAT solver.” In 2010 International Conference on High Performance Computing & Simulation, 306–13. https://doi.org/10.1109/HPCS.2010.5547116.

Musliu, Nysret, and Martin Schwengerer. 2013. “Algorithm Selection for the Graph Coloring Problem.” In Learning and Intelligent Optimization, edited by Giuseppe Nicosia and Panos Pardalos, 389–403. Berlin, Heidelberg: Springer Berlin Heidelberg.

Nichols, Daniel, Harshitha Menon, Todd Gamblin, and Abhinav Bhatele. 2023. “A Probabilistic Approach To Selecting Build Configurations in Package Managers,” November. https://doi.org/10.2172/2223030.

Nudelman, Eugene, Kevin Leyton-Brown, Holger H. Hoos, Alex Devkar, and Yoav Shoham. n.d. “Understanding Random SAT: Beyond the Clauses-to-Variables Ratio.” In Principles and Practice of Constraint Programming – CP 2004, edited by Mark Wallace, 438–52. Berlin, Heidelberg: Springer Berlin Heidelberg.

O’Mahony, Eoin, Emmanuel Hebrard, Alan Holland, Conor Nugent, and Barry O’Sullivan. 2008. “Using Case-Based Reasoning in an Algorithm Portfolio for Constraint Solving.” In Irish Conference on Artificial Intelligence and Cognitive Science, 210–16. Proceedings of the 19th Irish Conference on Artificial Intelligence; Cognitive Science.

Osama, Muhammad, Anton Wijs, and Armin Biere. 2021. “SAT Solving with GPU Accelerated Inprocessing.” In Tools and Algorithms for the Construction and Analysis of Systems, edited by Jan Friso Groote and Kim Guldstrand Larsen, 133–51. Cham: Springer International Publishing.

———. 2023. “Certified SAT solving with GPU accelerated inprocessing.” Form. Methods Syst. Des. 62 (1–3): 79–118. https://doi.org/10.1007/s10703-023-00432-z.

Pearl, Judea. 1984. Heuristics: Intelligent Search Strategies for Computer Problem Solving. USA: Addison-Wesley Longman Publishing Co., Inc.

Petrik, Marek, and Shlomo Zilberstein. 2006. “Learning parallel portfolios of algorithms.” Annals of Mathematics and Artificial Intelligence 48 (1-2): 85–106.

Pimpalkhare, Nikhil, Federico Mora, Elizabeth Polgreen, and Sanjit A. Seshia. 2021. “MedleySolver: Online SMT Algorithm Selection.” In Theory and Applications of Satisfiability Testing – SAT 2021, edited by Chu-Min Li and Felip Manyà, 453–70. Cham: Springer International Publishing.

Pulatov, Damir, Marie Anastacio, Lars Kotthoff, and Holger Hoos. 2022. “Opening the Black Box: Automated Software Analysis for Algorithm Selection.” In Proceedings of the First International Conference on Automated Machine Learning, 188:6/1–18. PMLR. https://proceedings.mlr.press/v188/pulatov22a.html.

Pulina, Luca, and Martina Seidl. 2019. “The 2016 and 2017 QBF Solvers Evaluations (QBFEVAL’16 and QBFEVAL’17).” Artificial Intelligence 274: 224–48. https://doi.org/https://doi.org/10.1016/j.artint.2019.04.002.

Redekopp, M., and A. Dandalis. 2000. “A Parallel Pipelined SAT Solver for FPGA’s.” In Field-Programmable Logic and Applications: The Roadmap to Reconfigurable Computing, edited by Reiner W. Hartenstein and Herbert Grünbacher, 462–68. Berlin, Heidelberg: Springer Berlin Heidelberg.

Rice, John R. 1976. “The Algorithm Selection Problem.” Advances in Computers. https://doi.org/10.1016/S0065-2458(08)60520-3.

Richter, Cedric, Eyke Hüllermeier, Marie-Christine Jakobs, and Heike Wehrheim. 2020. “Algorithm Selection for Software Validation Based on Graph Kernels.” Automated Software Engg. 27 (1–2): 153–86. https://doi.org/10.1007/s10515-020-00270-x.

Roberts, Mark, Adele E Howe, Brandon Wilson, and Marie desJardins. 2008. “What Makes Planners Predictable?” In ICAPS, 288–95.

Roussel, Olivier. 2012b. “Description of Ppfolio (2011).” Proc. SAT Challenge, 46.

———. 2012a. “Description of Ppfolio (2011).” Proc. SAT Challenge, 46.

Shavit, Hadar, and Holger H. Hoos. 2024. “Revisiting SATZilla Features in 2024.” In 27th International Conference on Theory and Applications of Satisfiability Testing (SAT 2024), edited by Supratik Chakraborty and Jie-Hong Roland Jiang, 305:27:1–26. Leibniz International Proceedings in Informatics (LIPIcs). Dagstuhl, Germany: Schloss Dagstuhl – Leibniz-Zentrum für Informatik. https://doi.org/10.4230/LIPIcs.SAT.2024.27.

Singer, Daniel, and Alain Vagner. 2006. “Parallel Resolution of the Satisfiability Problem (SAT) with OpenMP and MPI.” In Parallel Processing and Applied Mathematics, edited by Roman Wyrzykowski, Jack Dongarra, Norbert Meyer, and Jerzy Waśniewski, 380–88. Berlin, Heidelberg: Springer Berlin Heidelberg.

Sinz, Carsten, Wolfgang Blochinger, and Wolfgang Küchlin. 2001. “PaSAT — Parallel SAT-Checking with Lemma Exchange: Implementation and Applications.” Electronic Notes in Discrete Mathematics 9: 205–16. https://doi.org/https://doi.org/10.1016/S1571-0653(04)00323-3.

Sitaru, Ioana, and Madalina Raschip. 2022. “Algorithm Selection for Combinatorial Packing Problems.” In 2022 IEEE Congress on Evolutionary Computation (CEC), 1–8. Padua, Italy: IEEE Press. https://doi.org/10.1109/CEC55065.2022.9870417.

Smith-Miles, Kate, and Leo Lopes. 2012. “Measuring Instance Difficulty for Combinatorial Optimization Problems.” Computers & Operations Research 39 (5): 875–89. https://doi.org/https://doi.org/10.1016/j.cor.2011.07.006.

Somshubra Majumdar, Kunal Kukreja, Ishaan Jain. 2016. “AdaSort: Adaptive Sorting using Machine Learning.” International Journal of Computer Applications 145 (12): 12–17. https://doi.org/ 10.5120/ijca2016910726 .

Stuckey, Peter J., Thibaut Feydy, Andreas Schutt, Guido Tack, and Julien Fischer. 2014. “The MiniZinc Challenge 2008–2013.” AI Magazine 35 (2): 55–60. https://doi.org/10.1609/aimag.v35i2.2539.

Taitler, Ayal, Ron Alford, Joan Espasa, Gregor Behnke, Daniel Fišer, Michael Gimelfarb, Florian Pommerening, et al. 2024. “The 2023 International Planning Competition.” AI Magazine, 1–17.

Tange, O. 2011. “GNU Parallel - The Command-Line Power Tool.” The USENIX Magazine 36 (1): 42–47. https://doi.org/http://dx.doi.org/10.5281/zenodo.16303.

Thornton, Chris, Frank Hutter, Holger H. Hoos, and Kevin Leyton-Brown. 2013. “Auto-WEKA: combined selection and hyperparameter optimization of classification algorithms.” In Proceedings of the 19th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, 847–55. KDD ’13. New York, NY, USA: Association for Computing Machinery. https://doi.org/10.1145/2487575.2487629.

Torağay, Oğuz, and Shaheen Pouya. 2023. “A Monte Carlo simulation approach to the gap-time relationship in solving scheduling problem.” Journal of Turkish Operations Management 7 (1): 1579–90. https://doi.org/10.56554/jtom.1286288.

Tornede, Alexander, Lukas Gehring, Tanja Tornede, Marcel Wever, and Eyke Hüllermeier. 2023. “Algorithm selection on a meta level.” Machine Learning 112 (4): 1253–86.

Valenzano, Richard, Hootan Nakhost, Martin Müller, Jonathan Schaeffer, and Nathan Sturtevant. 2012. “ArvandHerd: Parallel Planning with a Portfolio.” In Proceedings of the 20th European Conference on Artificial Intelligence, 786–91. ECAI’12. NLD: IOS Press.

Vanschoren, Joaquin. 2019. “Meta-Learning.” In Automated Machine Learning: Methods, Systems, Challenges, edited by Frank Hutter, Lars Kotthoff, and Joaquin Vanschoren, 35–61. Cham: Springer International Publishing. https://doi.org/10.1007/978-3-030-05318-5_2.

Visentin, Andrea, Aodh Ó Gallchóir, Jens Kärcher, and Herbert Meyr. 2024. “Explainable Algorithm Selection for the Capacitated Lot Sizing Problem.” In Integration of Constraint Programming, Artificial Intelligence, and Operations Research, edited by Bistra Dilkina, 243–52. Cham: Springer Nature Switzerland.

Wager, Stefan, Trevor Hastie, and Bradley Efron. 2014. “Confidence intervals for random forests: The jackknife and the infinitesimal jackknife.” The Journal of Machine Learning Research 15 (1): 1625–51.

Wang, Qiang, Jiawei Jiang, Yongxin Zhao, Weipeng Cao, Chunjiang Wang, and Shengdong Li. 2021. “Algorithm selection for software verification based on adversarial LSTM.” In 2021 7th IEEE Intl Conference on Big Data Security on Cloud (BigDataSecurity), IEEE Intl Conference on High Performance and Smart Computing, (HPSC) and IEEE Intl Conference on Intelligent Data and Security (IDS), 87–92. https://doi.org/10.1109/BigDataSecurityHPSCIDS52275.2021.00026.

Williamson, David P., and David B. Shmoys. 2011. The Design of Approximation Algorithms. Cambridge University Press.

Woeginger, Gerhard J. 2002. “Exact Algorithms for NP-hard Problems: A Survey.” In, 185–207. Springer, Berlin, Heidelberg. https://doi.org/ 10.1007/3-540-36478-1_17 .

Wolpert, D. H., and W. G. Macready. 1997. “No Free Lunch Theorems for Optimization.” IEEE Transactions on Evolutionary Computation 1 (1): 67–82. https://doi.org/10.1109/4235.585893.

Wotzlaw, Andreas, Alexander van der Grinten, Ewald Speckenmeyer, and Stefan Porschen. 2012. “pfolioUZK: Solver description.” Balint Et Al.(Balint Et Al., 2012a), 45.

Wright, Marvin N., and Andreas Ziegler. 2017. “ranger: A Fast Implementation of Random Forests for High Dimensional Data in C++ and R.” Journal of Statistical Software 77 (1): 1–17. https://doi.org/10.18637/jss.v077.i01.

Xu, Lin, Holger H. Hoos, and Kevin Leyton-Brown. 2010. “Hydra: Automatically Configuring Algorithms for Portfolio-Based Selection.” In Proceedings of the Twenty-Fourth AAAI Conference on Artificial Intelligence, 210–16. AAAI’10 1. AAAI Press.

Xu, Lin, Frank Hutter, Holger H. Hoos, and Kevin Leyton-Brown. 2008. “SATzilla: Portfolio-Based Algorithm Selection for SAT.” J. Artif. Int. Res. 32 (1): 565–606.

Xu, Lin, Frank Hutter, Holger H Hoos, and Kevin Leyton-Brown. 2011. “Hydra-MIP: Automated algorithm configuration and selection for mixed integer programming.” In Proceedings of the 18th RCRA Workshop, 16–30.

Xu, Lin, Frank Hutter, Holger Hoos, and Kevin Leyton-Brown. 2012. “Evaluating Component Solver Contributions to Portfolio-Based Algorithm Selectors.” In Theory and Applications of Satisfiability Testing – SAT 2012, edited by Alessandro Cimatti and Roberto Sebastiani, 228–41. Berlin, Heidelberg: Springer Berlin Heidelberg.

Yuen, Shiu Yin, Chi Kin Chow, and Xin Zhang. 2013. “Which algorithm should I choose at any point of the search: An evolutionary portfolio approach.” In GECCO 2013 - Proceedings of the 2013 Genetic and Evolutionary Computation Conference, 567–74. https://doi.org/10.1145/2463372.2463435.

Yuen, Shiu Yin, Chi Kin Chow, Xin Zhang, and Yang Lou. 2016. “Which algorithm should I choose: An evolutionary algorithm portfolio approach.” Applied Soft Computing 40: 654–73. https://doi.org/https://doi.org/10.1016/j.asoc.2015.12.021.

Yuen, Shiu Yin, Yang Lou, and Xin Zhang. 2019. “Selecting Evolutionary Algorithms for Black Box Design Optimization Problems.” Soft Computing 23 (15): 6511–31.

Yun, Xi, and Susan L. Epstein. 2012. “Learning Algorithm Portfolios for Parallel Execution.” In Revised Selected Papers of the 6th International Conference on Learning and Intelligent Optimization - Volume 7219, 323–38. LION 6. Paris, France: Springer-Verlag.

ZHANG, HANTAO, MARIA PAOLA BONACINA, and JIEH HSIANG. 1996. “PSATO: a Distributed Propositional Prover and its Application to Quasigroup Problems.” Journal of Symbolic Computation 21 (4): 543–60. https://doi.org/https://doi.org/10.1006/jsco.1996.0030.

Zhang, Lintao, C. F. Madigan, M. H. Moskewicz, and S. Malik. 2001. “Efficient conflict driven learning in a Boolean satisfiability solver.” In IEEE/ACM International Conference on Computer Aided Design. ICCAD 2001. IEEE/ACM Digest of Technical Papers (Cat. No.01CH37281), 279–85. https://doi.org/10.1109/ICCAD.2001.968634.

Zhong, Peixin, M. Martonosi, P. Ashar, and S. Malik. 1998. “Accelerating Boolean satisfiability with configurable hardware.” In Proceedings. IEEE Symposium on FPGAs for Custom Computing Machines (Cat. No.98TB100251), 186–95. https://doi.org/10.1109/FPGA.1998.707896.